Random graph

Network science

Theory · History
Graph · Complex network · Contagion Small-world · Scale-free · Community structure · Percolation · Evolution · Controllability · Topology · Graph drawing · Social capital · Link analysis · Optimization Reciprocity · Closure · Homophily Transitivity · Preferential attachment Balance · Network effect · Influence
Types of Networks
Information · Telecommunication Social · Biological · Neural · Semantic Random · Dependency · Flow
Graphs
Vertex · Edge · Component Directed · Multigraph · Bipartite Weighted · Hypergraph · Random Cycle · Loop · Path Neighborhood · Clique · Complete · Cut Data structure · Adjacency list & matrix Incidence list & matrix
Metrics and Algorithms
Centrality · Degree · Betweenness Closeness · PageRank · Motif Clustering · Degree distribution · Assortativity · Distance · Modularity
Models
Random · Erdős–Rényi Barabási–Albert · Watts–Strogatz ERGM · Epidemic · Hierarchical
Browse
Topics · Software · Network scientists Graph theory · Network theory

In mathematics, a random graph is a graph that is generated by some random process.^[1] The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.

1 Random graph models
2 Properties of random graphs
3 Random trees
4 Interdependent Graphs
5 History
6 See also
7 References

Random graph models

A random graph is obtained by starting with a set of n vertices and adding edges between them at random. Different random graph models produce different probability distributions on graphs. Most commonly studied is the one proposed by Edgar Gilbert, denoted G(n,p), in which every possible edge occurs independently with probability p. A closely related model, the Erdős–Rényi model denoted G(n,M), assigns equal probability to all graphs with exactly M edges. The fastest known algorithm for generating the former model is proposed by Nobari et al. in.^[2] The latter model can be viewed as a snapshot at a particular time (M) of the random graph process $\tilde{G}_n$ , which is a stochastic process that starts with n vertices and no edges, and at each step adds one new edge chosen uniformly from the set of missing edges.

If instead we start with an infinite set of vertices, and again let every possible edge occur independently with probability p, then we get an object G called an infinite random graph. Except in the trivial cases when p is 0 or 1, such a G almost surely has the following property:

Given any $n+m$ elements $a_1,\ldots, a_n,b_1,\ldots, b_m \in V$ , there is a vertex $c\in V$ that is adjacent to each of $a_1,\ldots, a_n$ and is not adjacent to any of $b_1,\ldots, b_m$ .

It turns out that if the vertex set is countable then there is, up to isomorphism, only a single graph with this property, namely the Rado graph. Thus any countably infinite random graph is almost surely the Rado graph, which for this reason is sometimes called simply the random graph. However, the analogous result is not true for uncountable graphs, of which there are many (nonisomorphic) graphs satisfying the above property.

Another model, which generalizes Gilbert's random graph model, is the random dot-product model. A random dot-product graph associates with each vertex a real vector. The probability of an edge uv between any vertices u and v is some function of the dot product u • v of their respective vectors.

The network probability matrix models random graphs through edge probabilities, which represent the probability $p_{i,j}$ that a given edge $e_{i,j}$ exists for a specified time period. This model is extensible to directed and undirected; weighted and unweighted; and static or dynamic graphs.

For $M \simeq pn$ the two most widely used models, G(n,M) and G(n,p), are almost interchangeable.^[3]

Random regular graphs form a special case, with properties that may differ from random graphs in general.

Properties of random graphs

The theory of random graphs studies typical properties of random graphs, those that hold with high probability for graphs drawn from a particular distribution. For example, we might ask for a given value of 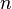$n$ and $p$ what the probability is that $G(n,p)$ is connected. 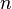In studying such questions, researchers often concentrate on the asymptotic behavior of random graphs—the values that various probabilities converge to as $n$ grows very large. Percolation theory characterizes the connectedness of random graphs, especially infinitely large ones.

Percolation is related to the robustness of the graph (called also network). Given a random graph of n nodes and an average degree $\langle k\rangle$ . Next we remove randomly a fraction $1-p$ of nodes and leave only a fraction $p$ . There exists a critical percolation threshold $p_c=1/\langle k\rangle$ below which the network becomes fragmented while above $p_c$ a giant connected component exists ^[1] ^[3] ^[4] ^[5] ^[6] .^[7]

(threshold functions, evolution of G~)

Random graphs are widely used in the probabilistic method, where one tries to prove the existence of graphs with certain properties. The existence of a property on a random graph can often imply, via the Szemerédi regularity lemma, the existence of that property on almost all graphs.

Random trees

Main article: random tree

A random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include uniform spanning tree, random minimal spanning tree, random binary tree, treap, rapidly exploring random tree, Brownian tree, and random forest.

Interdependent Graphs

Interdependent graphs or networks is a system of coupled networks where nodes of one or more networks depend on nodes in other networks. This dependency is enhanced by the developments in modern technology. Such dependencies may lead to cascading failures between the networks and a relatively small damage can lead to a catastrophic breakdown of the system. Blackouts are a fascinating demonstration of the important role played by the dependencies between networks. A recent study developed a framework to study the cascading failures in an interdependent networks system^[8]

History

Random graphs were first defined by Paul Erdős and Alfréd Rényi in their 1959 paper "On Random Graphs"^[6] and independently by Gilbert in his paper "Random graphs".^[7]

References

^ ^a ^b Béla Bollobás, Random Graphs, 2nd Edition, 2001, Cambridge University Press
^ Nobari, Sadegh; Lu, Xuesong; Karras, Panagiotis; Bressan, Stéphane (2011), "Fast random graph generation", Proceedings of the 14th International Conference on Extending Database Technology (Uppsala, Sweden: ACM) (11): 331–342, doi:10.1145/1951365.1951406, ISBN 978-1-4503-0528-0 Unknown parameter "keywords=" ignored; Unknown parameter "address=" ignored.
^ ^a ^b Bollobas, B. and Riordan, O.M. "Mathematical results on scale-free random graphs" in "Handbook of Graphs and Networks" (S. Bornholdt and H.G. Schuster (eds)), Wiley VCH, Weinheim, 1st ed., 2003
^ Newman, M. E. J. (2010). Networks: An Introduction. Oxford.
^ Reuven Cohen and Shlomo Havlin (2010). Complex Networks: Structure, Robustness and Function. Cambridge University Press.
^ ^a ^b Erdős, P. Rényi, A (1959) "On Random Graphs I" in Publ. Math. Debrecen 6, p. 290–297 [1]
^ ^a ^b Gilbert, E. N. (1959), "Random graphs", Annals of Mathematical Statistics 30: 1141–1144, doi:10.1214/aoms/1177706098 .
^ S.V. Buldyrev, R. Parshani, G. Paul, H.E. Stanley and S. Havlin (2010). "Catastrophic cascade of failures in interdependent network". Nature 464: 1025–8. doi:10.1038/nature08932.

Stochastic processes

Discrete time	Bernoulli process Branching process Chinese restaurant process Galton–Watson process Independent and identically distributed random variables Markov chain Moran process Random walk Loop-erased Self-avoiding Probabilistic cellular automata

Continuous time	Affine process Azéma's martingale Bessel process Squared Birth–death process Brownian motion Bridge Excursion Fractional Geometric Cauchy process Contact process Cox process Diffusion process Empirical process Feller process Fleming–Viot process Gamma process Hunt process Interacting particle systems Itō diffusion Itō process Jacobi (Wright–Fisher) process Jump diffusion Jump process Lévy process Local time Markov additive process McKean–Vlasov process Ornstein–Uhlenbeck process Poisson process Compound Non-homogeneous Schramm–Loewner evolution Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process Wiener process Wiener sausage Wishart process

Both	Branching process Gaussian process Hidden Markov model (HMM) Markov process Martingale Local Sub- Super- Random dynamical system Regenerative process Renewal process White noise

Fields and other	Brownian sheet Dirichlet process Gaussian random field Gibbs measure Hopfield model Ising model Markov random field Percolation Pitman–Yor process Point process Potts model Random field Random graph Random-cluster process

Time series models	Autoregressive conditional heteroskedasticity (ARCH) model Autoregressive integrated moving average (ARIMA) model Autoregressive (AR) model Autoregressive–moving-average (ARMA) model Generalized autoregressive conditional heteroskedasticity (GARCH) model Moving-average (MA) model

Financial models	Black–Derman–Toy Black–Karasinski Black–Scholes–Samuelson Chen Constant elasticity of variance (CEV) Cox–Ingersoll–Ross (CIR) Dothan Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market SABR volatility Vašícek

Actuarial models	Bühlmann Bühlmann–Straub Cramér–Lundberg Risk process Sparre–Anderson

Queueing models	Bulk Fluid Generalized queueing network M/G/1 M/M/1 M/M/c

Properties	Càdlàg paths Continuous Continuous paths Ergodic Exchangeable Feller-continuous Gauss–Markov Markov Mixing Piecewise deterministic Predictable Progressively measurable Self-similar Stationary Time-reversible

Limit theorems	Central limit theorem Donsker's theorem Doob's martingale convergence theorems Ergodic theorem Fisher–Tippett–Gnedenko theorem Large deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Moderate deviation principle Sanov's theorem

Inequalities	Burkholder Burkholder–Davis–Gundy Fefferman Kunita–Watanabe Langlart

Tools	Cameron–Martin formula Convergence of random variables Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itō integral Itō's lemma Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Meyer–Tanaka formula Optional stopping theorem Prohorov theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem Skorokhod space Snell envelope Stochastic differential equation Tanaka Stopping time Stratonovich integral Uniform integrability Wiener space Classical Abstract

Disciplines	Actuarial mathematics Econometrics Ergodic theory Extreme value theory (EVT) Large deviations theory Mathematical finance Mathematical statistics Probability theory Queueing theory Renewal theory Ruin theory Statistics Stochastic analysis Time series analysis

Daftar/Tabel -- stochastic processes topics

Contents